Year 3 to Year 6: A Square of Numbers
Can you put the numbers 1 to 8 into the circles so that the four calculations are correct?
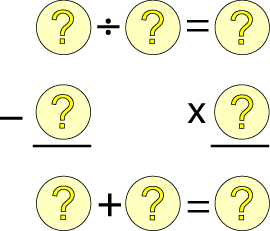
Firstly, you have to find the top left number, only 4 numbers are divisible between 1-8: 2, 4, 6 and 8. Then go across the problem.
Among these, 2 is only divisible by 1 and itself, meaning that either the number 2 is divided by or the answer, will have to be 2 as well. So 2 is ruled out.
The next one, 4, is only divisible by 1, 2 and 4. Divided by 1 gives 4 again; divided by 2 gives 2 again; and divided by 4 would be a repeat. 4 is ruled out.
6 can be divided by 2 and 3 (1 and 6 ruled out because they give repeats). If divided by 3, this gives the answer as 2, and now we look at the multiplication in the problem. Going down, 2 multiplied by 1 would be a repeat, 2 multiplied by 2 would be a repeat, multiplied by 3 would be a repeat, multiplied by 4 would give 8, which is OK. So 6 is possible at the top left corner.
Now we go back to 6, and do the subtraction going down. 6 can only be subtracted by the remaining numbers: 1, 5 and 7. 7 is bigger than 6 so that is ruled out. Subtracted by 1 would give 5, which when added to the last number remaining: 7, would give 12, not 8, as we have already worked out. So if it is 6-5, that would work since it gives 1, which when added to 7, gives 8. THIS IS THE FIRST SOLUTION.
We come to the second solution.
If we divide the 6 by 2, this gives 3. 3 (going down) multiplied by 1 would be a repeat, by 2 would give 6 again which has been used; by 3, that would be too big.
So now we come to the last possible number that can be used at the top left corner: 8. 8 can be divided by 2 and 4.
If divided by 2, this would give 4, and 4 going down (multiplication) times 1 would give 4, a repeat; multiplied by 2 would give 8 which was used already; and multiplied by 3 would be too big.
So we move on to 8 divided by 4, which gives 2. 2 times 1 is a repeat; times 2 is a repeat; times 4 gives 8, which has been used. But 2 times 3 gives 6, which hasn’t been used. So this is possible.
Back to the other side, the subtraction of 8. 8 can be subtracted by 1, 5 or 7, the remaining numbers.
Subtracted by 1 would give 7 and 7 plus 5, the last number, would be too big.
Subtracted by 5 would give 3, which has been used.
Subtracted by 7 would give 1, which when added to the last number remaining, 5 gives 6. THIS IS THE SECOND SOLUTION.

